Eksempel: Betongrør med frontmur

Oppgave

Vi skal finne kapasiteten til et betongrør under en vei og hvor høyt vannet vil stige ved en 200 års flom. Røret ligger der allerede, så dette er ikke en dimensjoneringsoppgave.

• Rørkulvert av betong.
• Innvendig diameter, D = 1,8 m.
• Lengde, L = 35 m.
• Innløpet i betonvegg med vingemurer, 90 graders hjørne ved innløpet.
• Det er ikke rist foran innløpet.
• Bekken nedstrøms kulverten er ca. 3 m bred og med sideskråning 1:2,5 (vertikal:horisontal). Bunnhellingen i bekken er 0,2 %
• Fra flomberegning vet vi 200-års flommen, Q₂₀₀ = 10 m³/s

Fremgangsmåte

Listen under viser hovedpunktene i beregningsgangen. Detaljene kommer under.

1. Samle opplysningene i et beregningsskjeema
2. Finn kapasitetskurven for innløpskontroll med et nomogram som passer til innløpet.
3. Finn vannstanden nedstrøms kulverten vha. Mannings formel.
4. Finn falltapene gjennom kulverten og kapasiteten for utløpskontroll.
5. Sett opp kurvene for innløps- og utløpskontroll
6. Fra kurvene finner du hvor mye vannstanden stiger ved Q200.

Innløpskontroll

Kapasiteten bestemmes fra nomogram som passer til formen på innløpet. Innløpet består av en vertikal betongvegg med vingemurer. I overgangen mellom mur og rør er det 90 graders hjørne.

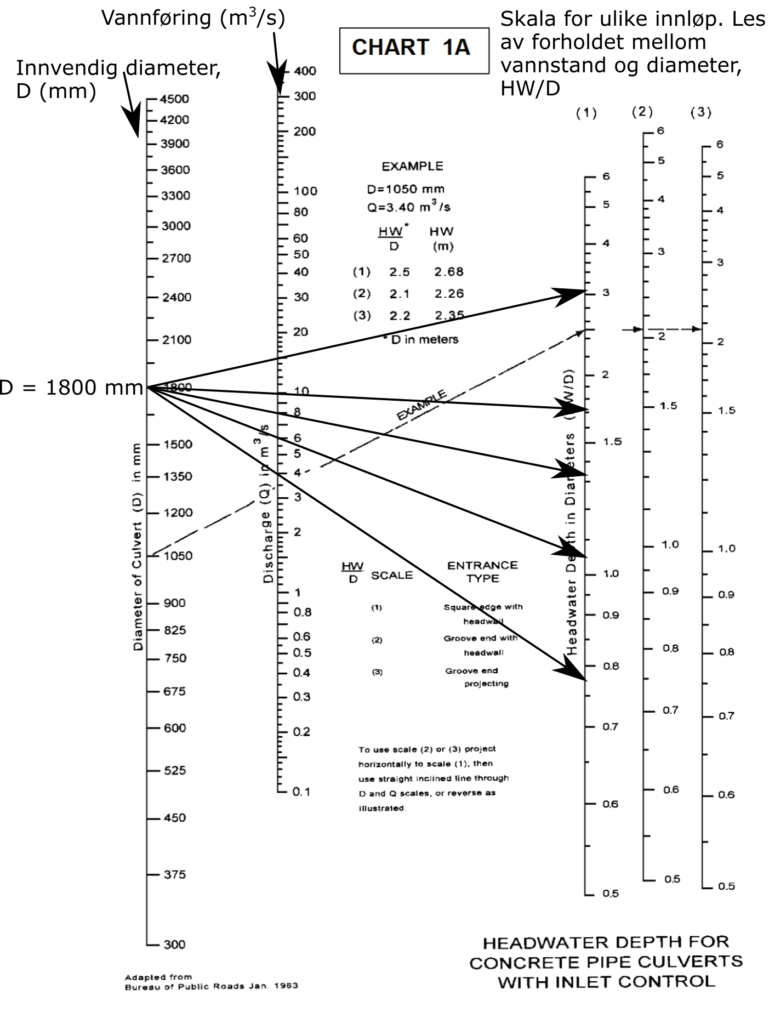
Chart 1A i Hydraulic Design of Highway Culverts gjelder betongrør. Frontveggen med 90 graders hjørne gjør at vi bruker scale 1. Vi velger noen vannføringer og leser av hvilken relativ vannstand de gir, se figuren under.

Forholdstallet HW/D leses av fra skala nr 1. Vannstanden, HW, beregnes ved å gange HW/D med kulvertdiameteren D. Tabellen under viser resultatet.

Vannføring, Q (m3/s)	Relativ dybde fra nomogran HW / D (-)	Vanndybde HW (m)
4,0	0,77	1,4
6,0	1,05	1,9
8,0	1,32	2,4
10,0	1,71	3,1
15,0	3,05	5,5

Vannstanden nedstrøms

For å beregne utløpskontroll må vi vite vannstanden rett nedstrøms utløpet. Hvis elveløpet har likt tverrsnitt og fall kan vi bruke Mannings-formel til å anslå vanndybden.

Vi vet at bekken er ca. 3 m bred og med sideskråning 1:2,5 (vertikal:horisontal), og at bunnhellingen er 0,2 %. Løpet er steinete, men med lite vegetasjon, så vi antar Mannings koeffisient, n = 0,033 (M = 30).

Vi velger å løse Mannings formel ved hjelp av diagram. (Du finner mer om beregningsmetoden her.) Først beregner vi uttrykket under for ulike vannføringer. Så leser vi av relativ dybde, y/b, fra diagrammet under. Tabellen viser resultatene.

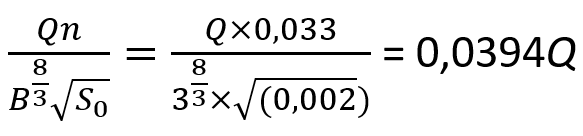
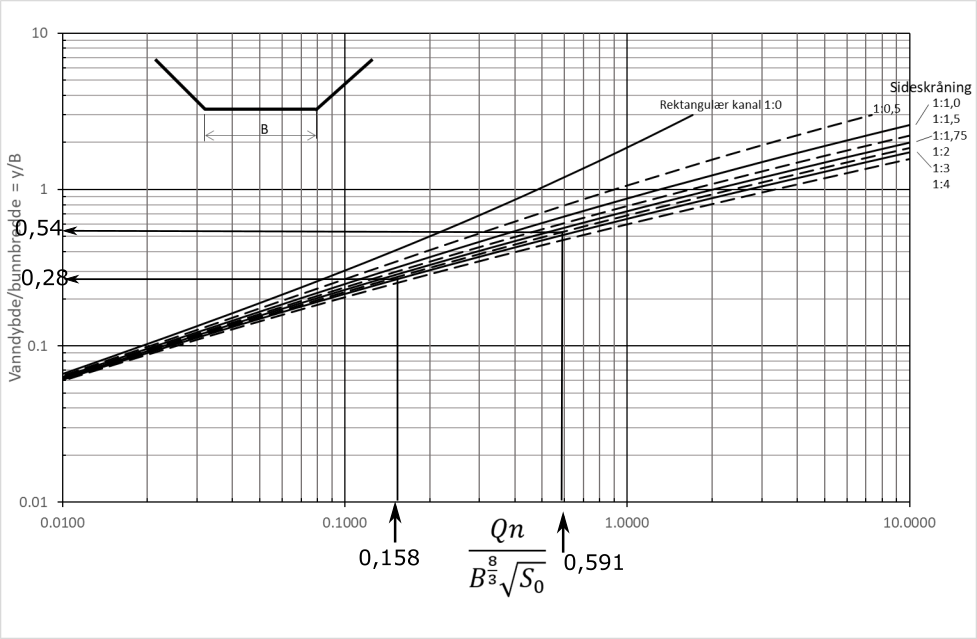
Vannføring, Q (m3/s)	Verdi fra formelen over (-)	Avlest fra diagram, y/B (-)	Vanndybde, y (m)
4,0	0,158	0,28	0,28*3 = 0,8 m
6,0	0,236	0,34	1,0
8,0	0,315	0,39	1,2
10,0	0,394	0,42	1,3
15,0	0,591	0,54	1,6

Innløpstap, utløpstap og friksjonstap

For utløpskontroll må vi beregne energitapene gjennom kulverten: innløpstapet, utløpstapet og friksjonstapet. (Beregningsmetoden er beskrevet her.)

Koeffisient for innløpstap

Frontvegg med rettvinklet (90 grader) hjørne gir et høyt innløpstap. Vi finner tapskoeffisienten fra tabellen under: k_e = 0,5.

Koeffisient for utløpstap

Vi setter koeffisient for utløpstap, k_o =1. Det er en vanlig forenkling som betyr at vi mister all hastighetsengergien. I de fleste tilfeller er energitapet mindre.

Friksjonstap

For å beregne friksjonstapet må vi anslå Mannings koeffisient. Velger n = 0,012 (M = 83,3) som typisk for et slitt betongrør.

Samlet energitap

Summen av innløpstap, utløpstap og friksjonstap beregnes med formelen under. (Utledningen finner du her.)

Vi forutsetter at røret er helt vannfylt. Da er hydraulisk radius R = A/P = D/4

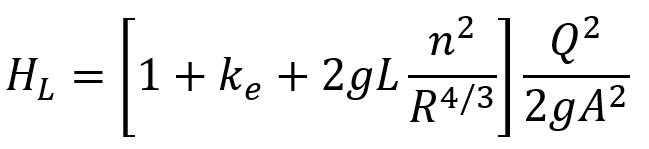
Vi setter inn: k_e = 0,5, L = 35 m, g = 9,81 m/s², n = 0,012, R = 0,45 m, A = 2,54 m² og får: H_L = 0,0141Q². Så setter vi inn ulike verdier av Q og finner totalt tap, H_L.

Tabellen under viser resultatet. Deltapene er vist hver for seg. Vi ser at singulærtapen (innløp & utløpstap) dominerer. Det er vanlig når kulverten er kort i forhold til diameteren.

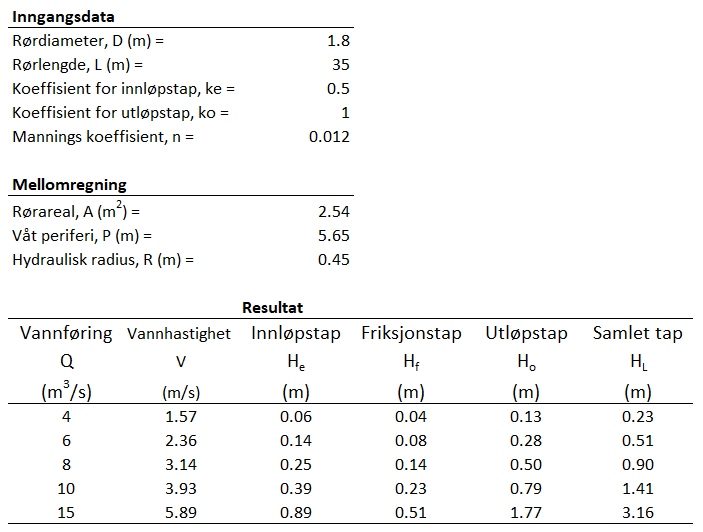
Kritisk dybde

Ved forenklet vannlinjeberegning for utløpskontroll trenger vi vannstanden ved utløpet som startvannstand for beregningene: (d_c +D)/2. Her er d_c kritisk dybde.

For et rør er det vanskelig å beregne kritisk dybde (critical depth), så vi bruker diagrammet under. Tabellen viser resultatet.

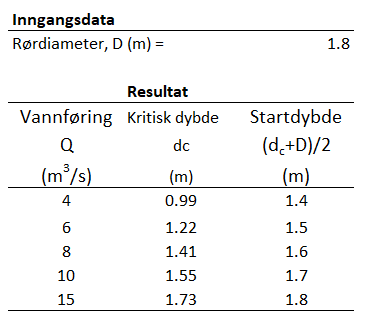
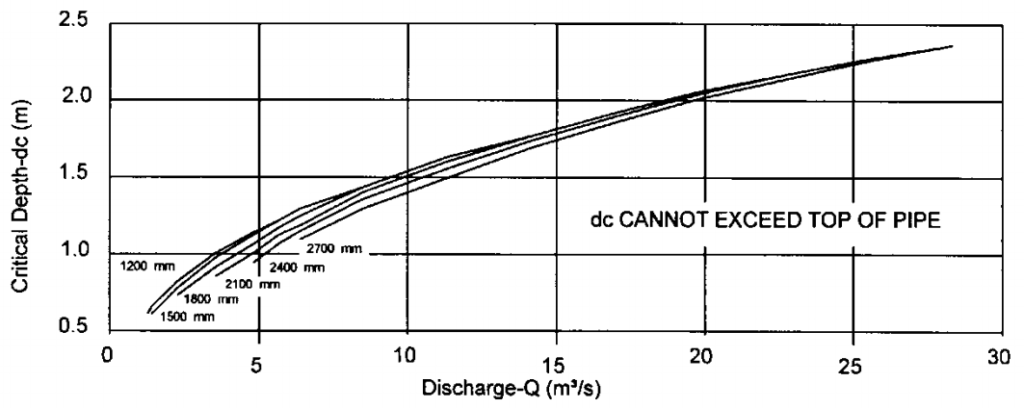
Beregningsskjema

For å holde oversikt over forutsetninger og resultat bør beregningene samles i et skjema, som vist under.

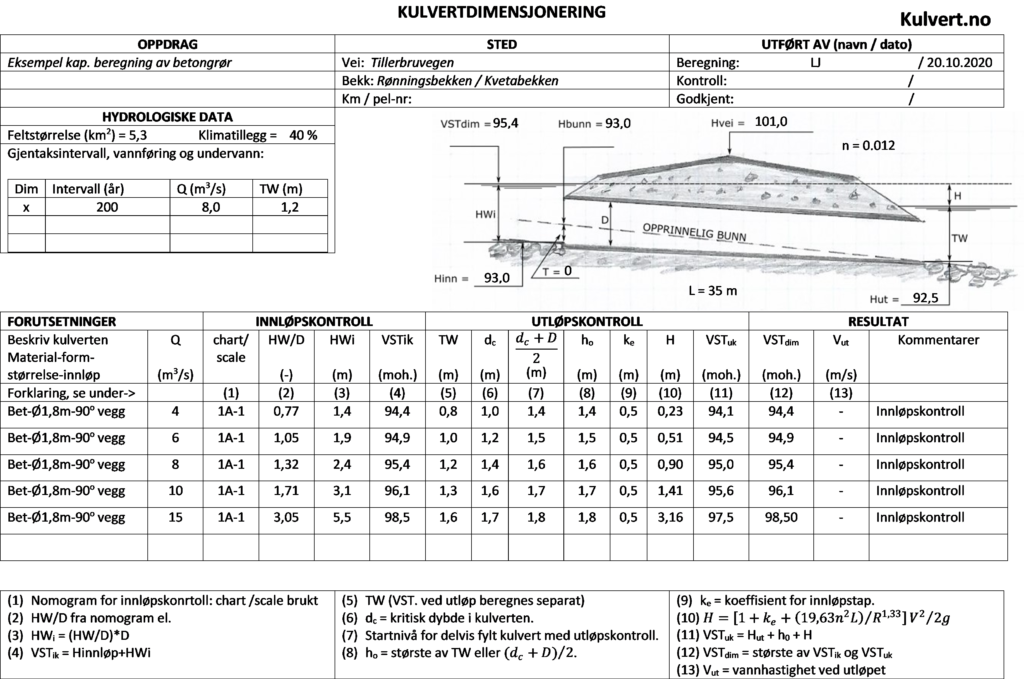
Kapasitetskurve -innløps- og utløpskontroll

Nå har vi beregnet vannstanden for ulike vannstander, både for innløpskontroll og utløpskontroll, og kan sette opp kapasitetskurven.

Vi ser at kurven for innløpskontroll hele tiden ligger over kurven for utløpskontroll. Det betyr at det er innløpskontroll som begrenser kapasiteten, og at kurven for innløpskontroll også er kapasitetskuven til kulverten.

I mange tilfeller kan disse kurvene krysse hverandre. Da følger kapasitetskurven den øverste kurven.

Som ekstra kontroll har jeg beregnet kapasiteten med HY-8 som er et program for kulvertberegning. HY-8 kurven ligger litt over kurven vi beregnet manuelt.

Vi skulle finne vannstanden for 200-års flommen, Q₂₀₀ = 10 m³/s. Fra skjemaet over eller kurven under finner vi at vannet må stige 3,1 m over bunnen av innløpet om vi skal få 10 m³/s gjennom røret. Det gir vannstand på 96,1 moh.