Anta at du skal beregne kapasiteten til en kulvert og trenger vannstanden i elven der kulverten munner ut. Hvis vi kan forutsette at det er normalstrømning i elven så kan vi bruke Mannings-formel til å beregne vanndybden.
I eksempelet viser jeg to fremgangsmåter for å løse Mannings-formel:
- Bruk diagram for normaldybde
- Løs Mannings-formel i regneark
Normalstrømning?
Elven har samme form, bredde og fall i flere hundre meter nedstrøms kulvertutløpet. Du kan derfor antat at det vil være normalstrømning slik at du kan bruke Mannings-formel til å beregne dybden.
Elvens størrelse, form og fall
Bunnen i elven er omtrent 9 m bred (B = 9 m). Elvebreddene heller ca. 1:2.
Fra kart og befaring anslår du hellingen til ca. 0,2 % (S0 = 0,003).
Ruhet – Mannings-n
Elvebunnen og breddene er dekket med grus. Elveløpet er uten vegetasjon, og det er lite vegetasjon på breddene.
Ut fra tabeller for Mannings-n anslår du at n = 0,025.
Dimensjonerende vannføring
Kulverten skal dimensjoneres for 200-års flom pluss 20 % tillegg for å ta hensyn til klimaendring. Du har gjort en fomberegningen og funnet at dimensjonerende vannføring er 1,2*Q200 = 35 m3/s.
Alternativ 1: Diagram for normaldybde
Bruk av diagrammet er heskrevet på siden om nedstrøms vannstand.
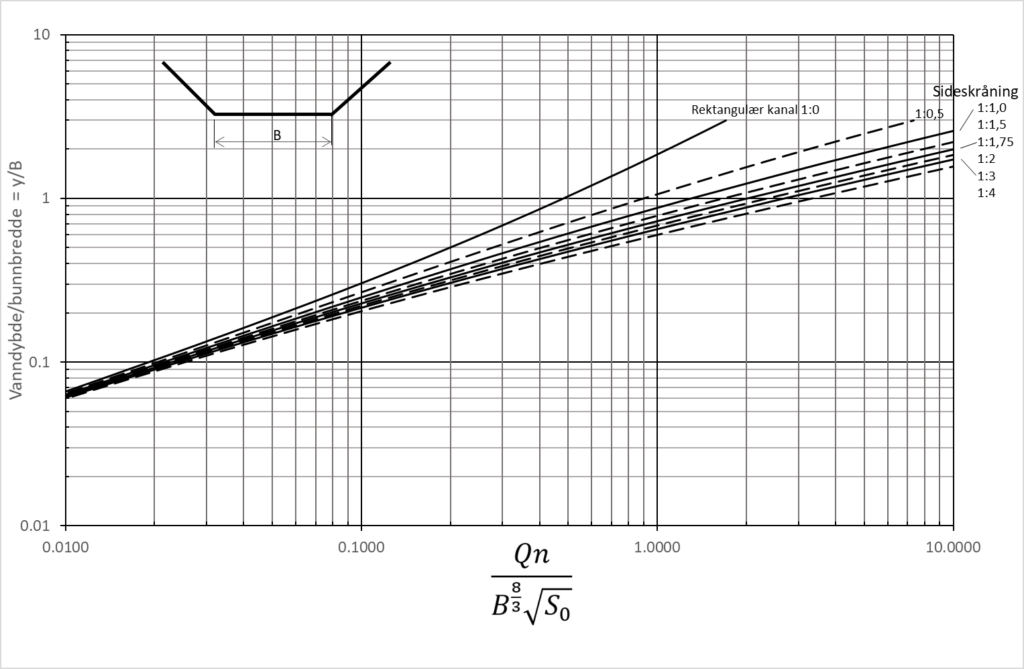
For trapesformede tverrsnitt kan vi bruke diagrammet under. Vi vet det som er nødvendig for å bestemme inngangsverdien på x-aksen, så går vi opp til kurven for sidehelling 1:2 og leser av dybde/breddeforholdet, y/B, på y-aksen.
Du setter inn Q = 35 m3/s, B = 9 m, So = 0,002 og n = 0,025 og finner at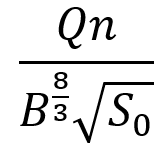 
= 0,056. I diagrammet går du opp fra 0,56 til kurven for 1:2 og leser av omtrent 0,17 – 0,18 på venstre akse (y-aksen). Det betyr at dybden er 17 % til 18 % av bunnbredden, dvs. y = 0,17 til 0,18 * 9 = 1,5 til 1,6 m.
Vanndybden i elven er ca. 1,55 m.
Alternativ 2. Løs Mannings-formel i regneark
Hvis du bruker Mannings-formel ofte kan de være praktisk å sette opp beregningene i et regneark. Der kan du enkelt endre inngangsverdiene på bredde, fall osv.
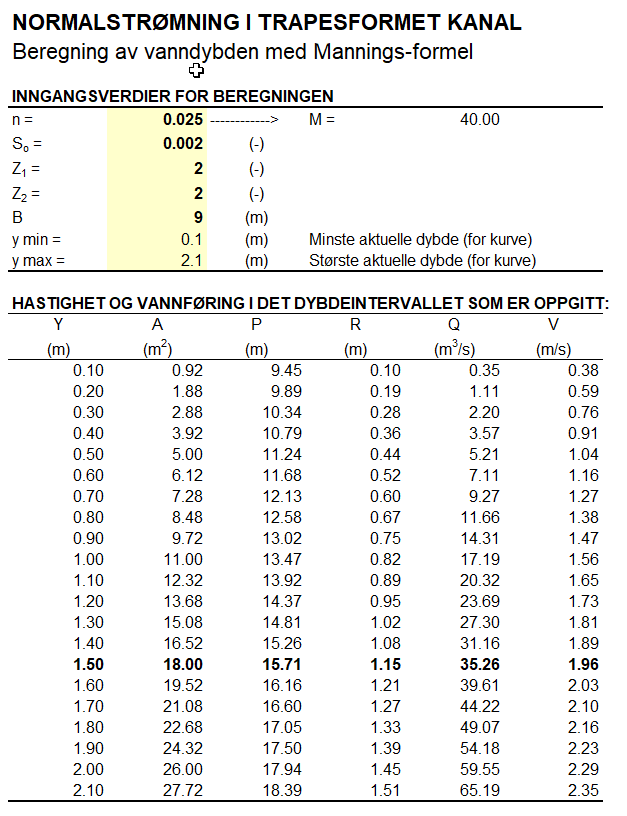
Jeg foretrekker å sette opp beregningene som vist under. Jeg bruker vanndybden, y, som uavhengig variabel og regner ut areal, våt periferi, hydraulisk radius og vannføring som funksjon av y. Så varierer jeg y til jeg finner den vannføringen jeg er interessert.
I dette tilfellet har jeg satt opp en tabell der jeg velger vanndybden (venstre kolonne) og beregner tilhørende vannføring. Z1 og Z2 er hellingen på elvebreddene (sidene i trapeset).
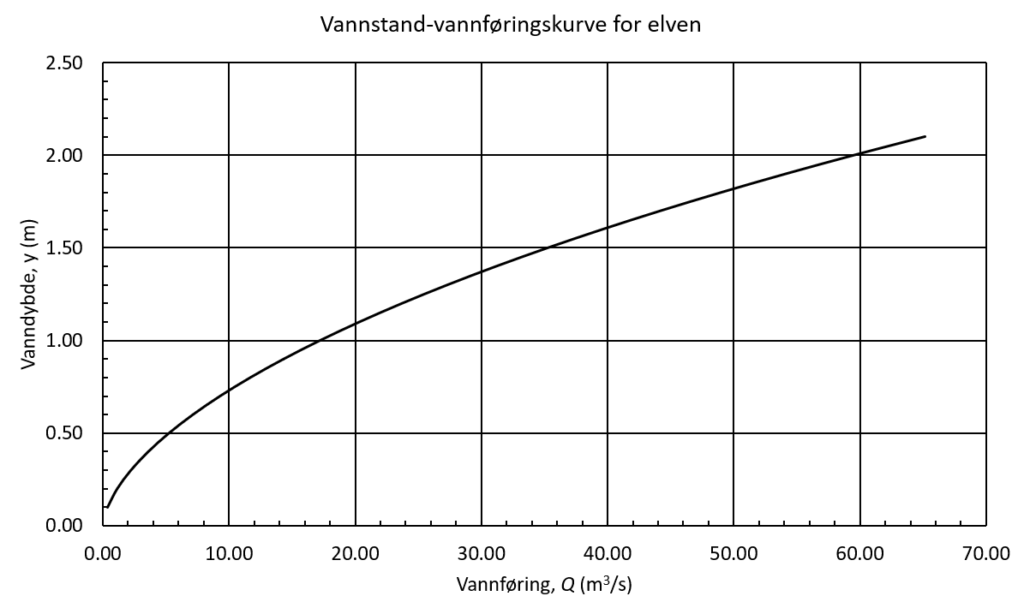
Jeg har også satt opp en kapasitetskurve, en vannstand-vannføringskurve for elva.
Fra tabellen under ser vi at når dybden er 1,5 m så er vannføringen ca. 35 m3/s. Det er ca. samme dybde som vi fant ved å bruke diagrammet i alternativ 1.
Advarsel – normalstrømning
Vær klar over at denne måten å bruke Mannings formel for å beregne vanndybden forutsetter normalstrømning. Det betyr at elva må ha konstant fall, tverrsnitt og ruhet slik at vannflaten og bunnen får samme fall i strømretningen.
Innsnevringer eller hindringer nedstrøms kan føre til oppstuving. Da er det ikke normalstrømning og vi kan heller ikke beregne dybden på den enkle måten vi gjorde over.